 Tylko u Nas
Tylko u Nas
Polska
Grozili dla żartu. Uruchomiono "procedurę napadową"
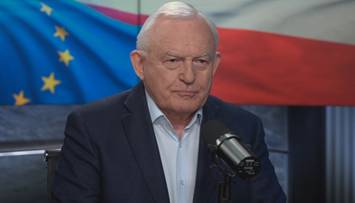 Tylko u Nas
Tylko u NasPolska
Miller o kulisach negocjacji. "Przeze mnie nie odbył się obiad u królowej"

Polska
Dziennikarze TVN24 przechodzą do Polsat News

Świat
Auta pędziły autostradą. Nagle spadły ze zbocza

Polska
Łoś wtargnął na autostradę. Pięć osób w szpitalu

Polska
Groźny incydent w stolicy. Prezydent: Potępiam atak

Polska
Oświadczenie prezydenta. "Chciałem stanąć tutaj z premierem. Nie skorzystał"

Świat
Katastrofa amerykańskiego F-16. Ostrzeżenie przed skażeniem
Polska
Premier nie przyjechał do prezydenta. Minister podał powód

Polska
20 lat Polski w Unii Europejskiej. Tak wyglądała droga do wspólnoty
 Tylko u Nas
Tylko u NasPolska
Minister podjął decyzję. "Dokumenty są gotowe"

Polska
20 rocznica wejścia Polski do UE. "Największy beneficjent unijnego budżetu"

Polska
Zażartował na lotnisku. Skreślono go z listy pasażerów
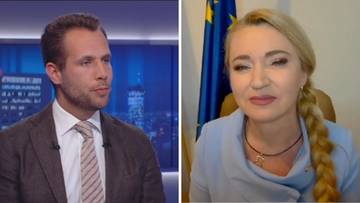 Tylko u Nas
Tylko u NasPolska
Sprzeczka posłów wokół premiera. "Proszę nie odpowiadać farmazonów"

Polska
PiS odkrywa karty. Wszystko jasne w sprawie Jacka Kurskiego

Świat
Pierwsza publiczna wizyta po diagnozie. Symboliczny gest króla Karola
 Tylko u Nas
Tylko u NasPolska
Formalnie nie istnieje. 34-latek "zniknął" w Polsce
 Tylko u Nas
Tylko u NasPolska
Pracownicy piekarni walczą o swoje. Nagle przestano płacić
 Tylko u Nas
Tylko u NasPolska
Akcja mobilizacyjna Ukraińców. "Nie będziemy brali udziału"

Świat
Rosyjska rafineria w ogniu. Media: To operacja specjalna

Polska
Europoseł nie odpuszcza. Awantura na Lewicy po kolejnym wpisie o Koniecznym

Polska
Prezydent przypomniał słowa papieża. "Ciągle są aktualne"

Polska
"Prezydent ponownie zaprosił premiera". Nowe informacje ws. spotkania

Polska
"Czekamy". Ambasador Izraela gratuluje polskiemu rządowi

Polska
Nowi dowódcy w polskiej armii. Jest decyzja A. Dudy
 Wypadek
WypadekPolska
Tragedia na stacji. Rowerzysta zginął pod kołami pociągu

Polska
Zaatakował kolegę z partii. "Żenujące obelgi"

Świat
Niespodziewanie zawiesili działalność. Pasażerowie utknęli na lotniskach

Polska
Utknęły na środku ronda. "Nikt się nie zatrzymał"

Świat
Słyszała "potwory" dobiegające ze ściany. "Jak z horroru"
 Tylko u Nas
Tylko u NasPolska
Burza wokół CPK. "Komunikowałbym to po wyborach"
 Aktualizacja
AktualizacjaPolska
Ruch prokuratury ws. Orlenu. D. Obajtek: Nigdy nie miałem niczego do ukrycia

Polska
Utrudnienia w ruchu, zmienione trasy. Warszawiacy mogą mieć kłopoty

Polska
Niebawem 32. Bieg Konstytucji 3 Maja. Zostały ostatnie numery startowe

Polska
Rada Ministrów zdecydowała ws. Krajowego Planu Odbudowy

Polska
J. Kaczyński o kwocie wolnej od podatku. "Można obliczyć, na ile oszukał D. Tusk"

Polska
Żarty nie na miejscu. Zatrzymani po wizycie w banku, wyciągnęli zabawkę

Świat
Incydent na spornym akwenie. Uszkodzono statek

Polska
"Pyton" z Rajska. Myśleli, że to egzotyczny i groźny wąż

Polska
Wdrapał się na dźwig i zaczął "demolkę". Ludzie zaalarmowali służby

Polska
Ostatni dzień składania PIT-ów. Surowe kary za brak oświadczenia

Polska
Głośno o "wyczynie" 20-latka. Zebrał rekordową liczbę punktów

Biznes
Ważna informacja ws. 800 plus. Dziś mija termin

Polska
Lawina zeszła tuż obok niego. Turysta uciekł w ostatniej chwili

Polska





























